Ocean Newsletter
第275号(2012.01.20発行)
- 関西大学社会安全学部学部長◆河田惠昭
- 東京大学大気海洋研究所教授◆道田 豊
- 東京大学海洋アライアンス海洋教育促進研究センター特任准教授◆丹羽淑博
- ニューズレター編集代表(総合地球環境学研究所・教授)◆秋道智彌
津波の正体を知る
[KEYWORDS] 津波の物理/海洋教育/数値実験東京大学海洋アライアンス海洋教育促進研究センター特任准教授◆丹羽淑博
2011年3月11日の東日本大震災では、三陸沖で日本観測史上最大となるマグニチュード9の大地震が発生し、それに伴い沿岸域を最大溯上高度40.5mの巨大津波が襲った。この大震災での死者・行方不明者は合わせて2万人近くにものぼり、犠牲者の約95%が津波にのまれて亡くなった。
このような津波被害を二度と繰り返さないためには、まずその第一歩として津波の正体を正確に知ることが非常に重要である。
津波とは何か
よく知られているように、津波は、沖合で地震が発生し海底の断層が隆起または沈降し、それに伴い海面が変動することによって発生する。東日本大震災では震源域で最初に波高が約5mの津波が励起されたが、同程度の波高を持つ通常の海の波(風波)は問題ないのに津波が甚大な被害をもたらすのは、津波が非常に大きな波長を持つからである。風波の波長が数mから数百mであるのに対し、津波の波長は桁違いに大きく数kmから数百kmに達する。津波が大きな波長を持つのは単純に断層の空間スケールを反映するからで、今回の大震災では断層が長さ約400km、幅約200kmに渡って動いた。
このような波長の相違は津波に伴う流れに大きな違いを生じさせる。短波長の風波では海水の流れが海面近くの深さに限定されるのに対し、水深に比べ十分長い波長を持つ津波では海面から海底までが海水が一様に動くようになる(図1)。大震災の津波が真っ黒な色に見えたのは、海全体を引きずる強い流れが海底の泥を巻き上げたためである。見渡す限りの海面が盛り上がり、海全体が動いて巨大な水の塊となって沿岸に一気に押し寄せるため、津波は大きな被害をもたらしたのである。
津波の物理
津波が海岸に到達する時間は震源距離と海底地形によって決まる。それは津波の伝播速度C が水深H に依存し![]() (g は重力加速度9.8m/s2)で与えられるからである。この公式から大震災の震源の水深は約1,600mだったので津波は初め時速450kmで伝わり、沿岸に近づくにつれ遅くなり、水深50m(三陸海岸の湾口付近の水深)では時速80kmで伝わったことがわかる。
(g は重力加速度9.8m/s2)で与えられるからである。この公式から大震災の震源の水深は約1,600mだったので津波は初め時速450kmで伝わり、沿岸に近づくにつれ遅くなり、水深50m(三陸海岸の湾口付近の水深)では時速80kmで伝わったことがわかる。
■図1 津波に伴う物理過程の模式図
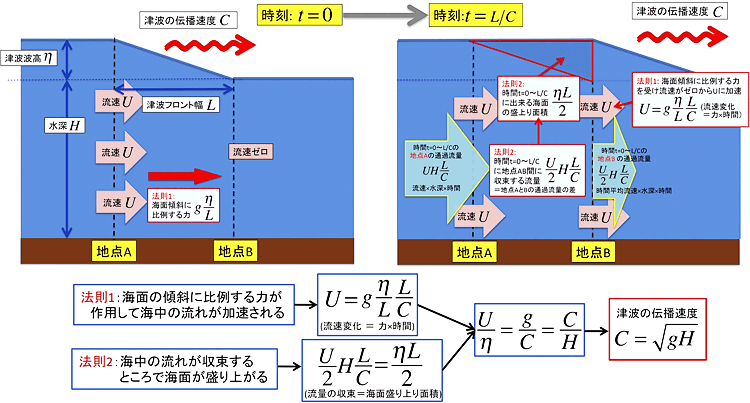
津波に伴う物理過程の模式図。地点Bに津波フロントの前部が到達した時刻t=0の様子(左上)とフロント後部が通過した時刻t=L/Cの様子(右上)。津波の伝播速度の導出方法のダイアグラム(下)。
図1は津波の物理過程の模式図である。津波の運動は二つの物理法則によって支配されている。「法則1」は海面が傾いた方向に傾斜に比例した力が作用して流れが加速されること、「法則2」は流れが収束するところで海面が盛り上がることである。図1(左上)は地点Bを津波のフロントが通過する直前、図1(右上)は通過直後の様子であるが、この津波に上記の二つの物理法則を適用することで伝播速度の公式![]() を導くことができる(図1(下)ダイアグラム)。
を導くことができる(図1(下)ダイアグラム)。
図1では津波がその波形を変えずそのまま伝播しているが、これも津波の重要な特徴の一つである。短波長の風波は伝播するにつれ波形が広がって徐々に波高が低くなる性質(分散性)を持っている。これは風波の伝播速度が波長により異なるためで、マラソンレースでランナーごとに走る速度が異なるためレース隊列が徐々に広がるのと同じ理屈である。それに対し、津波は波長によらず同じ速度![]() で伝播するため波形を崩さず非常に長い距離伝播できる。地球の裏側で発生したチリ地震大津波が太平洋を横断し日本沿岸に大きな被害をもたらしたのはそのためである。
で伝播するため波形を崩さず非常に長い距離伝播できる。地球の裏側で発生したチリ地震大津波が太平洋を横断し日本沿岸に大きな被害をもたらしたのはそのためである。
沖合で発生した津波が浅い沿岸域に近づき伝播速度が遅くなると、津波の前部が遅れだしそれに後部が追いつきエネルギーが前後の狭い幅に圧縮されるため波高が増大する。津波のエネルギーは波高の二乗![]() に波長は伝播速度
に波長は伝播速度![]() に比例するので、一波長分の津波エネルギーは
に比例するので、一波長分の津波エネルギーは![]() に比例する。この一波長分のエネルギーが保存されるので津波の波高
に比例する。この一波長分のエネルギーが保存されるので津波の波高![]() は水深の4乗根
は水深の4乗根![]() に反比例して大きくなる。つまり水深1,600mの沖合で発生した津波が水深50mの湾口付近まで伝わると波高は
に反比例して大きくなる。つまり水深1,600mの沖合で発生した津波が水深50mの湾口付近まで伝わると波高は![]() =2.38倍に増幅される。その上、さらに津波が三陸海岸のようなV字型湾の中を進行すると、湾幅Wが狭くなるにつれエネルギーが左右に圧縮される。このときは湾幅の平方根
=2.38倍に増幅される。その上、さらに津波が三陸海岸のようなV字型湾の中を進行すると、湾幅Wが狭くなるにつれエネルギーが左右に圧縮される。このときは湾幅の平方根![]() に反比例して波高が増幅される。大震災で三陸海岸の湾奥で波高15mを超える非常に大きな津波が観測されたのは、このような水深と湾幅の変化に伴う二つの増幅作用を受けたからである。
に反比例して波高が増幅される。大震災で三陸海岸の湾奥で波高15mを超える非常に大きな津波が観測されたのは、このような水深と湾幅の変化に伴う二つの増幅作用を受けたからである。
津波の数値実験
■図2 東日本大震災の津波を模した数値実験の結果
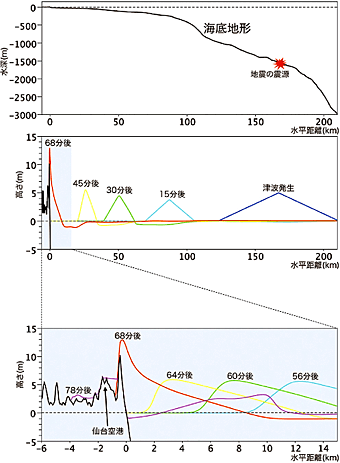
仙台空港を横切る緯度線(北緯38.13度)に沿った海底地形(上)、津波の発生から海岸到達までの振る舞い(中)、海岸付近の津波の拡大図(下)
図2は東日本大震災の津波の数値実験の一例である。仙台空港を横切る緯度線(北緯38.13度)に沿った海底地形(図2(上))の上に、震源位置を中心に海面の盛り上がりを与え、その後の津波の振る舞いを上記の物理法則に基づいて計算した。再現された津波は現実とほぼ同じく波高を増しながら68分後に海岸に到達し(図2(中))、それから陸上を約4km遡上した(図2(下))。この数値実験は湾幅の変化の効果を考慮しておらず正確な津波予測には使えないが、パソコンを使って津波の振る舞いを調べる教育素材として有用である。とくに津波に対し適切な避難行動をとるには津波の発生から到達までの全体的イメージを持つことが大切であり、そのためにも今後はこのような数値実験を積極的に活用した津波の防災教育を進めていく必要がある。(了)
第275号(2012.01.20発行)のその他の記事
- 東北地方太平洋沖地震を教訓とした地震・津波対策に関する専門調査会の活動 関西大学社会安全学部学部長◆河田惠昭
- ユネスコ政府間海洋学委員会(IOC)副議長への就任 東京大学大気海洋研究所教授◆道田 豊
- 津波の正体を知る 東京大学海洋アライアンス海洋教育促進研究センター特任准教授◆丹羽淑博
- 編集後記 ニューズレター編集代表(総合地球環境学研究所・教授)◆秋道智彌
